A/D Conversion

 

Introduction

We can obtain digital signal from analog one by performing analog to digital (A/D) conversion. Most signals of practical interest, such as speech, biological signals, seismic signals, radar signals, sonar signals, and various communications signals such as audio and video signals, are analog. To process analog signals by digital means, it is first necessary to convert them into digital form, that is, to convert them to a sequence of numbers having 6 finite precision. This procedure is called analog-to-digital (A/D) conversion, and the corresponding devices are called A/D converters (ADCs). Conceptually, we view A/D conversion as a three-step process.

A discrete‑time signal having a set of discrete values

A/D Conversion

Sampling, Quantization, Encoding

 

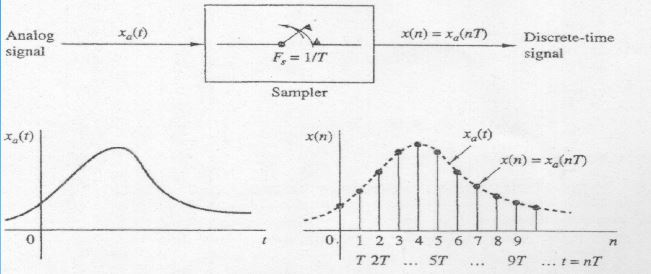
Sampling
Conversion of a continuous-time signal into a discrete time signal obtained by taking “samples” of the continuous-time signal as discrete-time instants T sampling interval, sec
Fs (=1/T) sampling frequency (sample/sec, Hz)

 

 

Sampling

Continuous-time signal	Discrete-time signal
Ω = 2πF Ω radian/sec F cycle/sec (Hz) F can have any value Rate of oscillation increases with Ω or F -∞ < Ω < ∞ -∞ < F < ∞	ω = 2πf ω radian/sample f cycles/sample (Hz) f is a rational number Rate of oscillation increases for a change of ω of 2π -π ≤ ω ≤ π -½ ≤ f ≤ ½

f = F/Fs
Fs   Δ sample/sec

 

 

Sampling Example: Aliasing

Quantization

Discrete leveling of DT signal (Approximation: rounding and truncation, ceiling)

Quantization
Quantization with one significant digit using Rounding

n	Discrete-time signal x(n)	x q (n) (Rounding)	Error e q (n) = x q (n)-x(n)
0	1	1.0	0.0
1	0.9	0.9	0.0
2	0.81	0.8	-0.01
3	0.729	0.7	-0.029
4	0.6561	0.7	0.0439
5	0.59049	0.6	0.00951
6	0.531441	0.5	-0.031441
7	0.4782969	0.5	0.0217031
8	0.43046721	0.4	-0.03046721
9	0.387420489	0.4	0.012579511

Quantization: Sinusoid 

Quantization Noise

Encoding
Representation of discrete (quantized) signals by symbols
              Mostly used is binary [0 1]
              Lowest value by 0 0 0 0 0 0 …
              Highest value may be 1 1 1 1 1 1 …
Representation of Discrete Time (DT) Signal:
x(n) = {…………………}
Some typical elementary DT Signals are:
              Unit step function: x(n) = u(n)
              Impulse function: x(n) = δ(n)
              Ramp function: x(n) = r(n)=n
              Power function: x(n) = an

 

 

 

 

 

Typical DT SP

Operations 

Elementary time domain operations

Scaling (amplification/attenuation): x(n) ax(n)

Time shifting (delay / advance): Folding / image / reflection:

x(n) x(n ± k) x(n) x(-n) Caution! x(-n-k) ≠ x[-(n+k)]

Time-scaling: x(n) x(an)
Addition: y(n) = x1(n)+x2(n)-x3(n)+.......
Subtraction, Multiplication, Division, Integration, Differentiation

Questions?

Comments!

Thank You !!!